sf.ops.Interferometer¶
-
class
Interferometer(U, mesh='rectangular', drop_identity=True, tol=1e-06)[source]¶ Bases:
strawberryfields.ops.DecompositionApply a linear interferometer to the specified qumodes.
This operation uses either the rectangular decomposition or triangular decomposition to decompose a linear interferometer into a sequence of beamsplitters and rotation gates.
By specifying the keyword argument
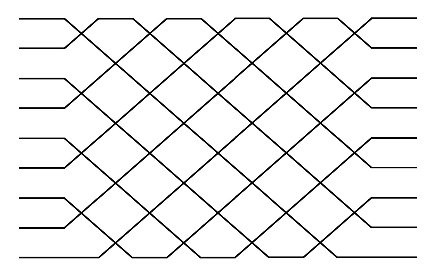
mesh, the scheme used to implement the interferometer may be adjusted:mesh='rectangular'(default): uses the scheme described in [23], resulting in a rectangular array of \(M(M-1)/2\) beamsplitters:Local phase shifts appear in the middle of the beamsplitter array. Use
mesh='rectangular_phase_endto instead commute all local phase shifts to the end of the beamsplitter array.By default, the interferometers are decomposed into
BSgateoperations. To instead decompose the interferometer using theMZgate, usemesh='rectangular_symmetric'.To use the compact rectangular decomposition of Bell and Walmsley (arXiv:2104.0756), use
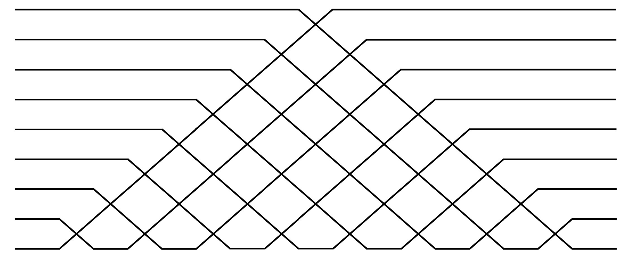
mesh='rectangular_compact'.mesh='triangular': uses the scheme described in [26], resulting in a triangular array of \(M(M-1)/2\) beamsplitters:To use the compact triangular decomposition, use
mesh='triangular_compact'.Local phase shifts appear at the end of the beamsplitter array.
- Parameters
U (array[complex]) – an \(N\times N\) unitary matrix
mesh (str) –
the scheme used to implement the interferometer. Options include:
'rectangular'- rectangular mesh, with local phase shifts applied between interferometers'rectangular_phase_end'- rectangular mesh, with local phase shifts placed after all interferometers'rectangular_symmetric'- rectangular mesh, with local phase shifts placed after all interferometers, and all beamsplitters decomposed into pairs of symmetric beamsplitters and phase shiftersrectangular_compact'- rectangular mesh, with two independant phase shifts placed inside each MZI, extra phase shifts on edges and at the input and output.'triangular'- triangular mesh'triangular_compact'- triangular mesh, with two independant phase shifts placed inside each MZI.
drop_identity (bool) – If
True, decomposed gates with trivial parameters, such that they correspond to an identity operation, are removed.tol (float) – the tolerance used when checking if the input matrix is unitary: \(|U-U^\dagger| <\) tol
Details and Conventions
The rectangular decomposition allows any passive Gaussian transformation to be decomposed into a series of beamsplitters and rotation gates.
Definition
For every real orthogonal symplectic matrix
\[\begin{split}O=\begin{bmatrix}X&-Y\\ Y&X\end{bmatrix}\in\mathbb{R}^{2N\times 2N},\end{split}\]the corresponding unitary matrix \(U=X+iY\in\mathbb{C}^{N\times N}\) representing a multiport interferometer can be decomposed into a set of \(N(N-1)/2\) beamsplitters and single mode rotations with circuit depth of \(N\).
For more details, see [23].
Note
The rectangular decomposition as formulated by Clements [23] uses a different beamsplitter convention to Strawberry Fields:
\[BS_{clements}(\theta, \phi) = BS(\theta, 0) R(\phi)\]Attributes
Extra dependencies due to parameters that depend on measurements.
-
measurement_deps¶ Extra dependencies due to parameters that depend on measurements.
- Returns
dependencies
- Return type
set[RegRef]
-
ns= None¶
Methods
apply(reg, backend, **kwargs)Ask a local backend to execute the operation on the current register state right away.
decompose(reg, **kwargs)Decompose the operation into elementary operations supported by the backend API.
merge(other)Merge the operation with another (acting on the exact same set of subsystems).
-
apply(reg, backend, **kwargs)¶ Ask a local backend to execute the operation on the current register state right away.
Takes care of parameter evaluations and any pending formal transformations (like dagger) and then calls
Operation._apply().- Parameters
reg (Sequence[RegRef]) – subsystem(s) the operation is acting on
backend (BaseBackend) – backend to execute the operation
- Returns
the result of self._apply
- Return type
Any
-
decompose(reg, **kwargs)¶ Decompose the operation into elementary operations supported by the backend API.
See
strawberryfields.backends.base.
-
merge(other)¶ Merge the operation with another (acting on the exact same set of subsystems).
Note
For subclass overrides: merge may return a newly created object, or self, or other, but it must never modify self or other because the same Operation objects may be also used elsewhere.
- Parameters
other (Operation) – operation to merge this one with
- Returns
other * self. The return value None represents the identity gate (doing nothing).
- Return type
Operation, None
- Raises
MergeFailure – if the two operations cannot be merged