Introduction¶

Strawberry Fields is an open-source framework for photonic quantum computing. In particular, Strawberry Fields allows for the following workflows:
Construct and simulate continuous-variable quantum photonic circuits. Provided simulators include highly optimized Gaussian, Fock, and Bosonic numeric backends, as well as a TensorFlow backend for backpropagation.
Compile and submit photonic circuits for remote execution on Xanadu’s quantum hardware, retrieve your results, and manage multiple jobs.
Use our high-level functions for graph and network optimization, machine learning, and chemistry applications — all executable on near-term hardware.
Get started¶
Follow the installation page to get Strawberry Fields up and running, then have a look at our quickstart guides, or jump over to the tutorials to see what you can do with Strawberry Fields.
Users interested in applications of photonic quantum computers should check out the Applications pages. Those wanting to dig deeper into the design of circuits can head to the Circuits page.
Developers can head to the Development guide to see how they can contribute to Strawberry Fields.
Quickstart guides¶
In the following sections you can learn more about the key features of Strawberry Fields:
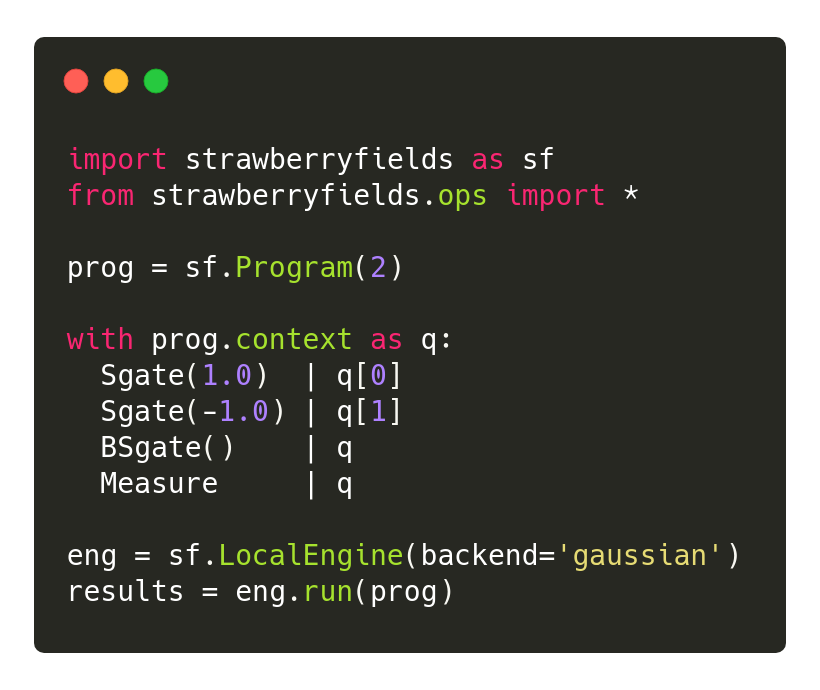
Circuits shows how to construct and simulate photonic circuits in Strawberry Fields, including applying quantum gates, performing measurements, and how to use our various simulator backends.
Operations outlines the various quantum photonic circuit building blocks provided in Strawberry Fields — including gates, state preparations and measurements.
States outlines the various statevector methods and attributes accessible when using the built-in simulators. These provide useful information and processing of the quantum state of the system.
Hardware and cloud gives an overview of building, submitting, and managing remote jobs on both hardware and cloud simulators through Strawberry Fields.
GBS datasets details the built-in datasets of pre-generated photonic samples provided by Strawberry Fields, for various graphs used in optimization, machine learning, and chemistry applications.